Zeno

Table of Contents

Zeno

Riwayat Hidup

Zeno lahir di Elea sekitar tahun 490. Ia adalah murid setia Parmenides. Sebagaimana gurunya, ia pun mempunyai peranan dalam politik kota Elea. Ia mengarang beberapa buku yang semua sudah hilang. Plato menceritakan bahwa bukunya yang terkenal dikarang pada usia muda. Dalam buku ini ia membela ajaran gurunya Parmenides, agaknya melawan kaum Pythagorean.

Ajaran

Aristoteles mengatakan bahwa Zeno menemukan dialektika. Istilah dialektika itu termasuk kata yang mendapat berbagai arti sepanjang sejarah filsafat. Aristoteles memaksudkan dengannya suatu cabang logika yang mempelajari perihal argumentasi yang bertitik tolak dari suatu hipotesis atau pengandaian. Dan memang itulah cara yang dipakai dalam peri argumentasi Zeno. Ia mulai dengan mengemukakan suatu hipotesis, yaitu salah satu anggapan yang dianut pelawan-pelawan Parmenides. Lalu ia menunjukan bahwa dari hipotesis itu harus ditarik kesimpulan-kesimpulan yang mustahil. Jadi, ternyata hipotesis semula tidak benar. Dan itu berarti bahwa kebalikannya harus dianggap benar. Menurut metode ini Zeno membuktikan bahwa adanya ruang kosong, pluralitas dan gerak sama-sama mustahil.

Argumentasi melawan ruang kosong

Andaikan saja, bahwa ruang kosong ada. Kalau begitu, ruang itu mempunyai tempatnya dalam ruang lain, yang harus ditempatkan dalam ruang lain lagi dan seterusnya sampai tak terhingga. Hal itu mustahil. Dari sebab itu mesti disimpulkan bahwa ruang kosong tidak ada (maksudnya sama dengan Parmenides: yang ada tidak ditempatkan dalam suatu yang lain).

Argumentasi melawan pluralitas

Jika suatu potongan garis terdiri dari titik-titik (jadi, jika kita menerima adanya pluralitas), maka potongan garis itu dapat dibagi-bagi. Karena setiap bagian sekurang-kurangnya mempunyai dua titik (yaitu titik pangkal dan titik akhir), pembagian dapat diteruskan sampai tak terhingga. Jadi, potongan garis itu terdiri dari titik-titik yang jumlahnya tak berhingga. Nah, titik-titik ini mempunyai panjang tertentu atau tidak. Kalau titik-titik mempunyai panjang tertentu, harus disimpulkan bahwa potongan garis itu tak berhingga panjangnya. Kalau titik-titik tidak mempunyai panjang tertentu, harus disimpulkan bahwa potongan garis itu tak berhingga pendeknya; dengan kata lain, sama dengan nol. Nah, kedua kesimpulan itu sama mustahilnya, karena ternyata suatu potongan garis mempunyai panjang yang tak berhingga. Dari sebab itu hipotesis semula tidak dapat diterima, yaitu bahwa suatu potongan garis terdiri dari titik-titik. Atau dengan kata lain, pluralitas tidak mungkin.

Argumentasi melawan gerak

Untuk membuktikan bahwa gerak tidak mungkin, Zeno memberi empat argumen. Inilah ajarannya yang paling masyhur. Aristoteles merupakan sumber utama untuk menentukan bagian ajaran ini. Disini ajaran pikiran Zeno sama dengan argumentasi-argumentasi di atas. Ia mulai dengan menerima pengandaian bahwa gerak memang ada, sebagaimana disaksikan pula oleh pancaindera. Dari situ ia menarik kesimpulan-kesimpulan yang mustahil. Dari sebab itu pengandaian semula tidak dapat dipertahankan dan kesaksian pancaindera tidak boleh dipercayai.
a) Pelari dalam stadion
Seorang pelari mau mencapai finis. Lebih dahulu ia harus menjalani setengah jarak stadion. Lalu setengah sisanya dan demikian terus-menerus sampai tak berhingga. Karena pelari harus menempuh bagian yang jumlahnya tak berhingga, maka tidak pernah ia akan sampai pada finis.

b) Akhilles dan kura-kura
Akhilles, jago lari dari mitologi Yunani, tidak dapat melewati kura-kura, binatang yang paling lambat, betapapun cepat larinya. Karena kura-kura berangkat sebelum Akhilles, maka lebih dahulu Akhilles harus mencapai titik dimana kura-kura berada sesaat ia berangkat. Setibanya di situ kura-kura sudah lebih jauh lagi dan seterusnya. Jarak antara Akhilles dan kura-kura selalu berkurang, tetapi tidak pernah habis.

c) Anak panah
Sesudah dipanahkan dari busurnya, anak panah tidak bergerak, tetapi diam. Karena pada tiap-tiap saat ia berada pada tempat tertentu, yang persis sama dengan panjangnya. Ia selalu berada antara kedua ujungnya dan karena itu senantiasa dalam keadaan diam. Pada saat berikutnya ia berada lebih jauh, tetapi disitu juga ia tidak bergerak, melainkan diam. Jadi, gerak semu itu tidak lain daripada suatu seri perhentian-perhentian.

d) Tiga deretan yang berjalan
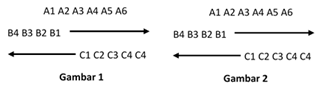
Dalam bentuk yang disampaikan kepada kita oleh Aristoteles argumentasi keempat ini tidak gampang dimengerti. Maksudnya barangkali dapat diterangkan sebagai berikut. Coba kita mengandaikan tiga deretan titik-titik; semua titik berdampingan satu dengan yang lain, sehingga tidak ada lowongan diantaranya (gambar 1). Deretan A tidak bergerak. Deretan B dan deretan C bergerak dalam arah yang berlawanan, tetapi dengan kecepatan yang sama, yakni demikian rupa sehingga pada satu saat atau bagian-waktu dijalani satu titik atau bagian-ruang. Satu saat sesudah gerak mulai, baik B1 maupun C1 telah menjalani satu titik dan masing-masing berdiri terhadap A4 dan A3 (gambar II). Jadi, B1 dan C1 sudah saling berlalu. Karena itu lebih dahulu mesti terdapat suatu saat lain, apabila B1 dan C1 persis berhadapan satu sama lain. Dengan demikian kita mendapati suatu saat baru yang lamanya adalah setengah dari saat yang tersebut tadi. Namun, menurut pengandaian semula, situasi yang dilukiskan oleh gambar II terjadi sesudah saat pertama gerak itu. Dari sebab itu kita harus menyimpulkan: 1/2 = 1. Atau dengan perkataan lain: sebelum saat pertama masih ada saat lain; saat pertama itu bukanlah saat yang pertama.  

Ket. klik warna biru untuk link

Download di Sini

Sumber.
Bertens, K. 1999. Sejarah Filsafat Yunani. Kanisius. Yogyakarta